- ...活動間隔・平均ずれ速度
- 地質学的な時間スケールにおけるずれの速度。
地震時にずれが生じる時の速度(破壊速度)ではない。
この報告書で,用語全般については文献[1]を参照。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
-
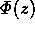 については,式(2.18)参照。
については,式(2.18)参照。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
-
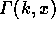 については,式(2.19)参照。
については,式(2.19)参照。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
-
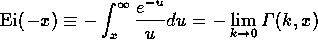 (積分指数関数)
(積分指数関数)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...この関数値は,正規分布表から,あるいは数値計算
- おおむね |z|<2.75程度までは,
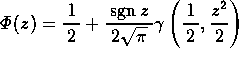 として計算する。ここで
として計算する。ここで 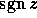 は zについての符号関数で,
z>0で 1,z=0で 0,z<0で -1を与える関数である。
は zについての符号関数で,
z>0で 1,z=0で 0,z<0で -1を与える関数である。
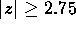 においては,
前述の式で
においては,
前述の式で 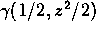 を
を 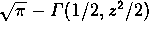 で
置き換えて計算する。なお,
で
置き換えて計算する。なお,
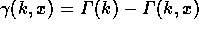 (第1種不完全ガンマ関数)である。
(第1種不完全ガンマ関数)である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
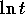 の平均を与える
の平均を与える - ちなみに,対数正規分布(2.22)の tについての平均は,
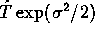 であり,
であり, 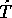 より若干大きい。
より若干大きい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
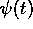 の台(support)
の台(support) - 関数 fの台とは,
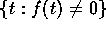 という集合の閉包のことである。
という集合の閉包のことである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...各パラメータの最尤値を求めた
-
最尤法については,付録B.1を,
パラメータ決定の実際については,付録B.1.2を参照。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
107#38
- 最新の地震から次回の地震までの間隔
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
125#54
- 最新の地震から次回の地震までの間隔
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
126#55
- 最新の地震から次回の地震までの間隔
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...また,前回の更に前のずれの量は分かっていないので
- 時間予測モデルの考え方に忠実に沿うならば,
前々回の地震の際のずれの量をもとにして,前回の地震の発生時期を推定すべきであるが,
現時点では不明であるため,断層の長さから推定される平均的な値を求めた。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
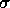 は,平均値の1/2〜2倍程度を示す0.3
は,平均値の1/2〜2倍程度を示す0.3 -
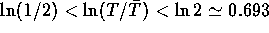 であるから,
であるから,
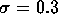 にとれば約
にとれば約 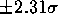 の範囲となって,
の範囲となって,
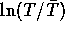 が正規分布に従うことを考慮すれば,
平均値の1/2〜2倍の範囲の事象は全事象の97.9%以上をカバーする。
因みに
が正規分布に従うことを考慮すれば,
平均値の1/2〜2倍の範囲の事象は全事象の97.9%以上をカバーする。
因みに 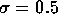 ならば全事象の83.4%以上がカバーされる。
ならば全事象の83.4%以上がカバーされる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...地震発生確率の再計算を行う
- 3.2.2においては,
地震発生間隔が指数分布に従う場合の計算もされているが,
この場合は確率が前回地震発生からの経過年数に依存しないため,
この議論を適用しても結果は変わらない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...HREF="node51.html#fig032">4.1参照
-
グラフが示唆するように,ガンマ分布の条件付き確率には1以外の上界があり,
その値は
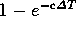 である。
これは生起率 cのPoisson過程における条件付き確率に他ならない。
この事実は,2.1.2で述べたように,
もともとガンマ分布の更新過程がPoisson過程の拡張
(r-1個おきの事象に着目したもの)であることから理解できる。
である。
これは生起率 cのPoisson過程における条件付き確率に他ならない。
この事実は,2.1.2で述べたように,
もともとガンマ分布の更新過程がPoisson過程の拡張
(r-1個おきの事象に着目したもの)であることから理解できる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...とすると
- 実際は,Hは対称行列であり,
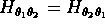 である。以後の計算では,
この事実を使っている。
である。以後の計算では,
この事実を使っている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
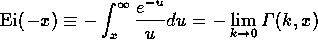 (積分指数関数)
(積分指数関数)
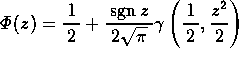 として計算する。ここで
として計算する。ここで