付録 改訂試案の解説
試案に寄せられた意見には、内容が専門的で、理解するのが容易ではないという意見がありました。この付録は改訂試案の理解を助けるための解説で、文責は地震調査委員会事務局(共同庶務)にあります。
陸上にある活断層や海溝沿いのプレート境界断層は、時々活動して、地震を起こしています。その活動の間隔は、断層によって長いのもあれば短いのもありますが、個々の断層にはそれぞれ固有の活動間隔があると考えられています。つまり、固有の活動間隔が例えば150年の断層は、150年よりも多少短い間隔で活動することもあり、また、それよりも多少長い間隔で活動することもありますが、平均すると
150年の間隔で活動を繰り返していると考えられます。この、多少短かったり長かったりするときの、そのばらつきの程度ですが、活動間隔の全データの約70%が固有の間隔の
4/5 倍から 5/4 倍の間に収まっています。つまり、地震が101回繰り返して発生したとすると、その発生間隔100回の内、約70回がその間に収まっています。全データの90%が収まる範囲でいうと、
2/3 倍から3/2倍の間になります。固有の間隔が150年の断層を例にとると、約70%が120年(=
150× 4/5)から 190年(≒ 150 × 5/4 )の間に、約90%が100年(150×2/3)から230年(≒150×3/2)の間に収まっています。今後、90%のデータが収まっている範囲を使うことにすると、次の地震は前回の地震から見て「100年後かもしれないし、230年後かもしれない」ということになります。
活断層の活動時期のばらつきから100年後とか230年後とか言うのは、過去において発生した地震の間隔から経験的に言えることです。その予測の幅を狭くするためには、経験に頼るだけでなく、地震を起こす地下の状態を詳しく調べ、この状態ならあと何年後に地震が起きるということが分かるようにすることが必要です。しかし、今日の地震学は残念ながらそこまでは到達していません。地下の状態を詳しく知るための研究を進めることはもちろん重要なことですが、現在の到達点において言える最大限のことを追及することも大事なことです。試案はそういう立場でとりまとめられています。
一口に100年後とか230年後とか言っても、そこには130年もの開きがあり、これは人間社会の時間からすれば人の一生の長さを越える、おおきなあいまいさです。150年間隔の断層では130年の開きですんだのですが、陸域の活断層の多くは1,000年を越える間隔で活動しています。仮に、150年の10倍の1,500年の間隔で活動する断層でしたら、あいまいさも10倍の1,300年にもなります。こんなあいまいな情報は、社会が地震防災を考えるうえで、役にたたないと考えるかもしれませんが、必ずしもそうとばかりは言えません。活動の可能性を確率を用いて表現することにより、役にたつ場合もあるのです。この小文では、確率を用いた表現の仕組みを解説しています。また、確率で表現された内容の役立て方についても言及しています。
目次に戻る
ある活断層の平均活動間隔が分かり、そして前回の活動時期が分かれば、次回の活動時期もある程度は予想できることになります。ちょうど一定の間隔で活動を繰り返していれば次の時期は正確にわかるのですが、間隔にはばらつきがつきものです。こうしたばらつきがあるときは、次の活動時期は確率を使って表現することになります。
確率を使うことの意味を考えるために、おみくじをひく場合のことを考えてみましょう。おみくじ100本のなかに凶が3本あるとします。このおみくじをひくとき、凶をひく確率は3%です。「今後30年間にこの活断層が活動して地震を起こす確率は3%」と言うときの3%も、おみくじの3%と同じ「危なさ」です。さて、確率の計算の仕方ですが、おみくじの場合、凶のおみくじをひく確率は、おみくじをつくった人におみくじの本数とそのなかの凶の本数を聞けば分かります。これは非常に簡単に計算できます。しかし、活断層が活動して起きる地震の場合は、そんなに簡単ではありません。計算には、次のようなやや複雑な手続をふむ必要があります。
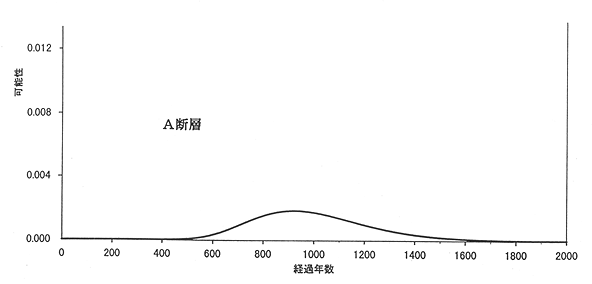
平均活動間隔が1,000年の活断層があるとしましょう。仮にA断層と呼びます。A断層が、ちょうど今、活動したとします。地震を起こしたわけです。では、A断層がこの次に活動するのはいつになるでしょうか。第1図がそれを説明するためのものです。この図は試案の(2.1)式をグラフに描いたもので、横軸は今後の経過年数、縦軸は活動する可能性の大きさを表しています。活動する可能性は600年後くらいから次第に大きくなり、平均活動間隔の1,000年後の少し前で最も大きくなっています。それを過ぎると次第に小さくなっていきます。平均活動間隔の1.5倍の1,500年もたてば、きっとその前にもう地震を起こしているでしょうから、可能性は小さくなっています。
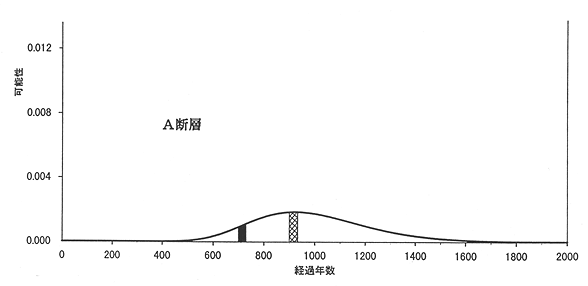
第1図を用いて、A断層が、例えば700年後から730年後までの間に活動する確率を求めることができます(第2図)。それは、700年のところと730年のところに縦線を引き、
(700年の縦線と730年の縦線の間にある山の面積)÷(山全体の面積)
が、その確率になります。同様に、900年後から930年後までの間に活動する確率でしたら
(900年の縦線と930年の縦線の間にある山の面積)÷(山全体の面積)
になります。こうした計算から、A断層が次に活動する確率は、900年〜930年の方が700年〜730年よりも大きいことがわかります。同じ時間幅をとって比較するならば、時間が平均活動間隔だけ経過した頃に活動する確率が最も大きく、それよりも早く活動する確率や、もっと遅く活動する確率は小さいことが、第2図から直ちに理解できるでしょう。
また、こうした計算の仕組みからわかるように、対象とする期間が長いほど、確率は大きくなります。例えば、900年後から930年後までの間に活動する確率は、900年後から1,000年後までの間に活動する確率よりも小さいのです。これは当然ではありますが、重要な性質です。つまり、30年間使う設計の構造物と100年間使う設計の構造物とがあった場合、後者は地震にあう確率が高いので、それに応じた耐震設計が必要になるということを意味しています。
さて、以上のことは、最初に「A断層が、ちょうど今、活動したとします」と述べましたように、断層が活動した直後に考えたことです。断層が活動して、しばらくたった後に考えると、事情は少し変わってきます。我々が関心のある断層は必ずしも活動した直後のものばかりではなく、活動後、多かれ少なかれ時間が経過していますから、上の確率計算の考え方はそのままでは適用できません。どう考えるべきかは後に
(4) で述べますが、その前に、少し寄り道をします。
目次に戻る
断層が活動して、しばらくたった後の確率計算を考える前に、第1図に描かれた山の形について述べておきます。第1図に示された山の形が対数正規分布と呼ばれる形です。試案ではその他にも、ガンマ分布、ワイブル分布、二重指数分布が述べられています(それぞれ、試案の(2.2)式、(2.3)式、(2.4)式に対応)が、これらの山の形は、対数正規分布の形と微妙な違いはありますが、よく似ています。よく似ているからこそ、試案の4.1節に述べられているように、いずれがいいモデルかについて、明確な違いが見出せなかったのです。また、試案で議論されているσ(シグマ)は、山全体のなだらかさを表します。第1図はσの値として、試案の4.1節で推奨された0.23を使っています。σの値が大きくなるほど、山はなだらかになり、かつ、山の頂上の位置は少しずつ左に寄っていきます。σの値が小さくなると山がけわしくなります。この場合には、活動の平均活動間隔に近いところほど、地震を起こす可能性が大きくなることになり、活動がより規則的に起こっていることに相当します。
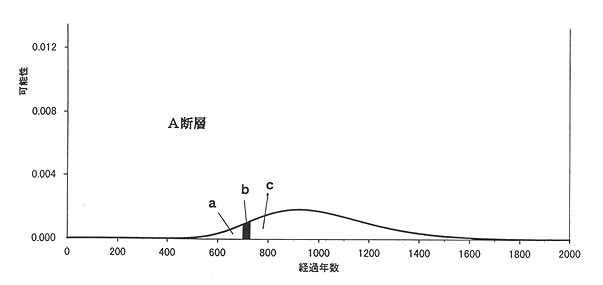
さて、断層が活動してからしばらくたった後の確率計算の考え方について述べます。例として、A断層が活動してから700年経過しているとします。その時点から30年間(活動した時点から見ると、700年後から730年後までの間)に活動する確率を考えてみましょう。A断層が活動した直後の時点だったら、第3図のbの部分の面積を使って、
(bの面積)÷(aの面積+bの面積+cの面積)
で、計算することは先に述べました。しかし、前回の活動から700年経過した時点では、地震はこれまでの700年間は発生しないまま時間が過ぎ去ったのですから、第3図のaの部分は考えにいれてはいけないのです。つまり、確率は
(bの面積)÷(bの面積+cの面積)
で計算すべきなのです。これが、断層が活動してからしばらくたった後の確率計算の考え方で、これは試案の(2.12)式に相当します。こうして計算された確率を条件つき確率といいます。これは、「700年間、地震は発生していない」という条件のもとで確率計算をしているので、そう呼ばれています。試案で使われている確率の数値は、更新過程によるものはすべて、条件つき確率の考え方で計算しています。
条件つき確率の考え方は、次のような例にも見られます。10本のおみくじの中に吉が9本、凶が1本あるとしましょう。最初におみくじをひいて凶をひく確率は1/10=0.10ですが、実際にひいたところ吉だったとします。これが、700年間、地震が発生しなかったことに対応します。2回目に凶をひく確率は、くじが1本減っていますので、1/9=0.11・・・に増えています。上の割算で、割る数からaの面積を除いて(bの面積+cの面積)としたのも、実際に地震が発生していないという条件を考えに入れているからなのです。
試案の表4.2で、断層の活動を注意喚起するための指標がいくつか提案されています。そのなかの指標(3)に集積確率というのがありますが、これは、第3図で、
(aの面積)÷(aの面積+bの面積+cの面積)
のことです。つまり、前回活動から700年たっているという第3図の例では、その時点における集積確率が上式で与えられるのです。これは、言葉で言えば「その時点までにすでに地震が発生していてしかるべき(発生しているはずの)確率」ということになります。例えば、現在時点で集積確率が30%だというのは、これは上述のおみくじの例でいうと、3回ひいて3回とも吉(地震が起こらない)だった状態に相当します。集積確率が大きいほど、凶をひく日が近づいています。
地震発生という現象は、ばらつきはあるものの、ある一定の時間間隔で繰り返して発生する現象であると考えています。ですから、地震が発生しないまま時間が経過すると、地震発生の確率はどこまでも大きくなって100%に近づいていくと考えられます。ところが試案の4.1節で述べられているように、対数正規分布モデルでは、活動間隔の2倍を過ぎたあたりから確率が下がっていきます。このため、このモデルは、一見、良いモデルではないと考えるかもしれません。しかし、よく考えてみると、確率が下がり始める時点での累積確率(すでに地震が発生していてしかるべき確率)を調べてみると、99.9%を上回ってほとんど100%になっています。つまり、確率が下がり始めるまで地震を起こさないままでいることは、千回に1回も起きないような非常に稀なことなのです。採用するモデルに、そんなにも稀な現象までをもうまく説明することは期待しなくてもいいと考えられます。つまり、確率が下がり始める現象は、対数正規分布モデルの適用限界を越えたところの話だと言えます。
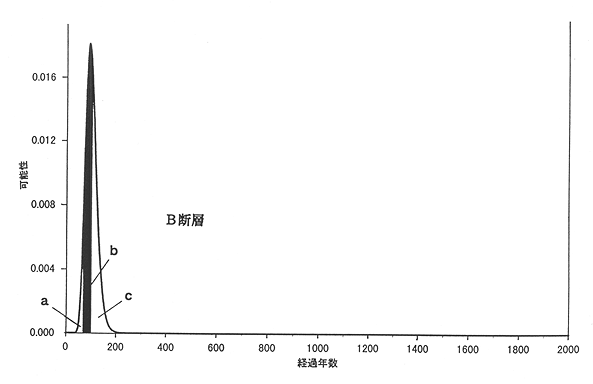
ある時間幅での地震発生確率は、活動間隔の長い断層は短い断層に比べて、確率の数値が大きくならないように感じますが、その理由を考えてみます。第1図〜第3図に示した山の形は、平均活動間隔が1,000年のA断層について、地震発生の可能性の大きさが時間の経過とともに、どう変化していくかを示していました。ここで比較のために、活動間隔の平均が100年であるB断層を考えましょう。第4図がB断層の活動する可能性の大きさを表しています。
第1図〜第3図と第4図は、縦軸と横軸のスケールは等しくしてあります。また、確率を計算するときの分母にくる山全体の面積も等しくしてあります。こうしておけば、確率は分子にくる面積そのものの広さで比較することが可能になり、便利です。これらの図で、活動間隔が違うことに対応して山の頂上の位置が違っています。また、山のなだらかさは大いに違っていますが、実はσはまったく同じ値0.23を使っています。使ったσが同じ値なので、山の高さが最大になってから平均活動間隔の約0.3倍の時間が過ぎると、山の高さは両者とも半分になります。山の高さが半分になるまでの実際の年数は、第3図が約300年、第4図が約30年です。実は、第3図の横軸の時間目盛を1/10にし、かつ、縦軸の可能性の目盛を10倍にすると、第4図の山とちょうど重なるのです。
さて、以上の準備のもとに、最初の疑問 −ある時間幅での地震発生確率は、活動間隔の長い断層は短い断層に比べて、確率が大きくならないように感じる− を考えてみます。A断層もB断層も活動間隔の0.7倍の時間、つまり、それぞれ、700年、70年の時間がたつまで地震を起こさなかったとします。そこで、今後30年間の地震発生確率を、条件つき確率の
(bの面積)÷(bの面積+cの面積)
で計算します。これで計算した地震発生確率は、100年間隔で繰り返して活動するB断層の方が大きくなるということは、第3図及び第4図を比較してすると明らかです。活動間隔が長い断層の地震発生確率が大きくならないように感じるというのは、こうした仕組みによるものです。なお、A断層が今後300年間に活動する確率と、B断層が今後30年間に活動する確率なら、ちょうど等しくなります。
確率の考え方のこうした仕組みそのものが不合理だと考える方もいるかもしれません。しかし、平均活動間隔が100年の断層の活動間隔のばらつきが、例えば、30年だとするとき、平均活動間隔が1,000年の断層の活動間隔のばらつきは300年になると考えるのは、むしろ合理的であり、そう考える方が実際のデータによく合っているのです。これは、平均活動間隔が長い断層ほど、活動時期を(統計的に)予測することは難しいということに通じています。
先に、第1図〜第3図と第4図で、確率計算するときに便利なように、確率計算の分母にくる山全体の面積は等しくしてあると述べました。こうしたことにより、平均活動間隔が短いB断層の活動の可能性の方が大きいように見えるので、これを不合理と考える方もいるかもしれません。しかし、平均活動間隔が短い断層の方が、実際のところ、活動の可能性がより大きいのです。例えば、10万年という非常に長い期間を考えてみましょう。平均活動間隔からすると、この期間にA断層は100回活動したはずですが、B断層はその10倍の1,000回も活動したことになります。この意味において、平均活動間隔が短いB断層の方が活動の可能性が大きい、「危ない」断層であるといえるでしょう。10万年という時間は非日常的な長さの時間で、その間に地震が何回起きるかなどという情報は、地震防災のうえでは全くと言っていいほど役にたたないものです。今後30年間に地震の起きる可能性の大きさを確率で表現するのは、そうした非日常的な長さの時間についての情報を地震防災において少しでも使いものになるように工夫した結果なのです。
試案の表4.1には、各断層の今後30年間の発生確率がまとめられています。この確率の数値への理解を深めるため、卑近な例と比較してみます。天気予報で言う降水確率は馴染みの深い生活情報ですが、これは、ある地域で、ある時間帯に1mm以上の降水が期待される確率のことです。通常の生活感覚からすると、10%や20%のときは傘を携帯しないで外出することが多いようですが、その時間帯に戸外に出ることが多い場合や、雨に濡れたら損害が大きい場合には、少し慎重になって傘を携帯するのが、確率の賢い利用方法です。逆に、50%などという高いときでも、戸外に出ることがほとんどない場合や、濡れたときの損害よりも傘という荷物を増やすことの煩わしさが大きい場合には、雨が降らない方に賭けるのもいいでしょう。
さて、試案の表4.1に掲載されている内陸の活断層の多くは、活動間隔が長いので、10%以下の数字が並んでいます。これらの地震への対策を考える場合、降水確率のように数字が小さいから、そういう地震は起きないものとして対策は必要ない、というのは正しい考え方ではありません。実際、表4.1の下半分に掲載された内陸の活断層沿いの地震はすべて、30年確率が10%程度以下のときに発生していることが読みとれます。ここで対象としている地震はマグニチュードで言えば7から8クラス(試案の表4.1の右端の欄を参照)の、大きな災害をもたらす地震です。降水確率を利用する場合とは違って、生命にかかわることなので、雨に降られて服が濡れた、だけではすまないのです。
消防白書によりますと、平成8年の日本の人口1億2,500万人のうち、火災で罹災した人が約9万1千人いたそうです。これは、類焼も含めて、自宅がなんらかの被害にあった人の数で、単なる山林等の火災は含まれていません。将来もこの割合が続くとすると、今後30年間に火災で罹災する確率は約2%だという計算になります。また、交通安全白書によりますと、平成8年の道路交通事故による死者と負傷者とを合わせると約95万人となります。これから、今後30年間に交通事故により死亡または負傷する確率は約20%だということになります。これらの数字は、活断層が今後30年間に活動する確率と比較することが可能です。万が一の火災のときのために消火器を備えたり、保険に入っている人は多いと思われます。また、各家庭や学校では、幼児や児童に、交通事故にあわないための躾や教育が繰り返されています。
30年確率で2%や20%の出来事に、このように備えているとすれば、それ以上の確率が見込まれる地震にも備えを怠らないというのが合理的な態度と言えるでしょう。
確率の数字は、限りある予算を地震防災対策につぎ込むべきか否か、つぎ込むとすれば、どこで起きる地震への対策を優先させるべきか、あるいは、如何ほどの予算をかけるのが妥当か、というような判断をする時の基礎資料としても利用できます。
なお、試案の表4.1に掲載されている数字そのものは、暫定的なデータにもとづく予備的な結果ですので、現段階で防災情報として理解するのは必ずしも適切ではありません、との断り書きが、試案の意見募集要項にあることをお忘れなく。
まず、試案の中では、しばしばポアソン過程が引合いにだされ、ポアソン過程のモデルはデータをうまく説明できない、と述べられています(例えば4.1節)。それはそのとおりなのですが、ポアソン過程は非常に単純なモデルなので、対数正規分布等のモデルと比較する対象として登場しています。ポアソン過程を表す式は試案の(2.5)式で、その山の形は図2.1に指数分布という呼び名で示されています。これだけでは単純さがわかりませんが、図4.2から図4.10までに掲載されている直線を見れば、その単純さがわかるでしょう。つまり、ポアソン過程のモデルによれば、地震が発生する条件つき確率(図4.2から図4.10でいうところの危険率)は時間によらずに、一定なのです。地震の発生は、放射性元素の崩壊のように、一定の確率(割合)で全く偶然に起きる、というモデルです。このモデルの場合、平均活動間隔が100年の断層の危険率(地震発生回数/年)は1/100に、1,000年の断層のそれは1/1000と、非常に単純になります。これは、数10万年以上という超長期間でみたときの1年間当たりの地震の平均発生回数にほかなりません。
ポアソン過程との比較は図4.2〜図4.10で行われ、その結果が表4.2で注意喚起するための指標としてまとめられています。表4.2で、指標(5)がポアソン過程による危険率そのものです。指標(1)と指標(2)がポアソン過程による危険率と対数正規分布モデルによる危険率(図では地震発生回数/年で表しています。これまで条件つき確率と称してきたものと同じ)とを比較したものです。指標(1)はポアソン過程による危険率を越えてからの年数を時間軸(横軸)に沿って見たもの、これに対して指標(2)はポアソン過程による危険率をどれくらい上回っているかを危険率の軸(縦軸)に沿って見たものです。これらの指標は、その断層の現在の危険率を、数10万年以上にわたる超長期的な平均危険率と比較したものといえます。指標(3)の集積確率はすでに説明したように、「現在までにすでに地震が発生していてしかるべき確率」です。指標(4)は、すでに説明した対数正規分布モデルでは活動間隔のおおむね2倍を過ぎたあたりで極大値を持つという性質に関連しています。現在の危険率をその最大値と比較することにより、危険さを正当に伝えたいという意図があ
ります。
目次に戻る
ある期間内に地震の起きる確率は、地震発生の可能性の絶対的な大きさを表すものです。内陸の活断層の多くは平均活動間隔が長いので、前述のように、30年確率はあまり大きな値になりません。その値が10%程度以下のときでも、実際には地震が発生しています。したがって、こうした地震への対策を考える場合、10%以下の確率でも、それを直ちに小さいとみなすのは正しい見方ではありません。確率の数字だけでは伝えられない地震発生の可能性に対し、注意を喚起するために幾つかの指標が提案されました。この指標は、ある値を越えるまでは地震は起きず、また、その値を越えたら必ず地震が起きる、というものがいいものといえます。しかし、仮にそのようなものが存在するならば、過去の経験にもとづく統計のみで地震発生時期の特定が可能だ、ということになってしまいます。そういう事態はちょっと考えられません。実際の地震発生時期を知るためには、過去の経験を統計的に調べることによって地震発生時期をある程度の幅に追い込んだ後、その幅のなかで地震や地殻変動等の地球物理的な観測をおこなって、その観測結果を解釈するモデル
を構築することによって予測の確度あげていくという進み方が望ましいと考えられます。地震調査委員会が現在進めている長期評価は、地震発生時期をある程度の幅に追い込むのに貢献できます。この評価は、地震学の現在の到達点からの重要な社会還元のひとつであると言えます。こうした情報を最大限に利用できるようにしたいものです。
第1図:A断層の活動可能性の大きさの変化。A断層の平均活動間隔を1,000年とし、活動する可能性の大きさが経過年数とともに変化する様子を、A断層が活動した直後の時点で考えたもの。試案の(2.1)式で、mをln(1000)≒6.91、σを0.23として計算した。横軸がt、縦軸がf(t;
m,σ)。
第2図:A断層が活動する確率の計算方法。700年後から730年後までの間に活動する確率は、700年の縦線と730年の縦線の間にある山の面積(黒塗り部分)を山全体の面積で割ることによって計算できる。900年後から930年後までの間に活動する確率も同様に網目部分を山全体の面積で割ることによって計算できる。
第3図:A断層が活動する条件つき確率の計算方法。A断層が活動してから700年経過した時点でまだ活動していない場合、その時点から30年間(活動した時点から見ると、700年後から730年後までの間)に活動する条件つき確率は (bの面積)÷(bの面積+cの面積) で計算される。また、試案の表4.2の指標(3)の集積確率とは
(aの面積)÷(aの面積+bの面積+cの面積) を意味する。これは「700年後の時点までにすでに地震が発生していてしかるべき確率」を意味する。
第4図:B断層が活動する条件つき確率の計算方法。B断層の平均活動間隔は100年として、山の形は試案の(2.1)式で、mをln(100)≒4.61、σを0.23として計算した。山全体の面積は第3図と等しくしてある。B断層が活動してから70年経過した時点でまだ活動していない場合、その時点から30年間(活動した時点から見ると、70年後から100年後までの間)に活動する条件つき確率は、第3図の場合と同様に (bの面積)÷(bの面積+cの面積) で計算される。
目次に戻る

前の文書へ戻る
地震調査研究推進本部のホームページへ戻る