注
「この資料は、成果を社会に活かす部会での検討に資する観点で、事務局が作成したメモです。従って、ここに示した内容（数値を含む。）については、部会での検討以外の利用については、責任を負うことはできません。引用はしないようにお願いします。」

資料　成５−（４）

「長期的な地震発生確率」に関する指標について（事務局メモ）

１．「（改訂試案）長期的な地震発生確率の評価手法について」で提唱されている指標

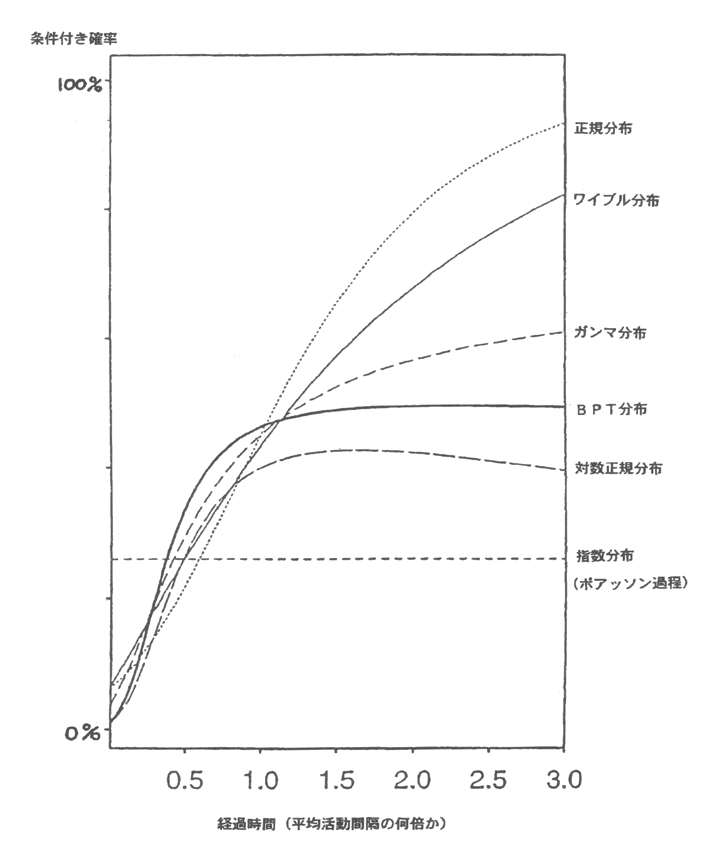
　現在、地震調査委員会長期評価部会に設けられた長期確率評価手法検討分科会において、長期的な地震発生確率を評価する手法を取りまとめる議論がなされているが、分科会では、近年提唱され、物理的説明がなされているＢＰＴ（Ｂｒｏｗｎｉａｎ Ｐａｓｓａｇｅ Ｔｉｍｅ）分布モデルを対数正規分布に代わる候補とする方向で議論が進んでいる。そこで、「（改訂試案）長期的な地震発生確率の評価手法について」（長期評価部会，１９９９）で提唱されている指標にならって、指標の定義をＢＰＴ分布に適用できるように、下のように再定義して一覧表（表１）を作成した。

　また、ＢＰＴ分布と対数正規分布は、改訂試案のデータセットに対して適用すると、実用上はほぼ同じとみなしうるほどよく似た挙動を示すことが確認されている。ここで示した指標も、対数正規分布用に作られたものとよく似た値を示す。他方、対数正規分布モデルでは、平均活動間隔の２倍程度の時間を過ぎると確率が下がっていってしまうという性質があるが、ＢＰＴ分布モデルでは、一定の値に漸近していくという性質がある。

（１）指標の定義

・指標（１）：

前回の地震発生時からの評価時点までの経過時間（Ｂ）、前回の地震発生時から指数分布（ポアッソン過程：ランダムな地震発生を仮定したモデル）の危険率（一年あたりの地震発生数）を超えるまでの時間（Ａ）として、

「年」はＢ−Ａ、「比」はＢ／Ａ

（注）全国共通のばらつきのパラメータμ＝０．２３を用いると、Ａは平均活動間隔の約０．７１倍になる。

・指標（２）：

評価時点の危険率と、ポアッソン過程の危険率との比

・指標（３）：

前回の地震発生時から評価時点までの集積確率（それまでに地震が発生していてしかるべき割合）（％）

・指標（４）：

評価時点から３０年間での、条件付き確率と、ＢＰＴ分布での収束値（無限大時間経過時点における確率）との比

・指標（５）：

ポアッソン過程での危険率

（２）指標の性質

　　ア　特定の断層についての指標と時間経過の関係

　ある断層について考えると、時間の経過とともに指標（１）〜（３）はいずれも、徐々に増加する。指標（４）は、ある程度の時間が経過すると一定値に収束するという性質を持つ。指標（５）は、断層に固有の値（平均活動間隔の逆数）で一定である。

　　イ　平均活動間隔が長い断層についての指標の性質

　今後３０年間に地震が発生する確率がほぼ同じで、平均活動間隔が異なる架空の断層を考え、表１にその指標を例示した。表のとおり、ほぼ同じ可能性で地震が発生するものであっても、指標（１）〜（５）はいずれも全く異なる値を示すので、平均的な活動間隔が大きく異なる断層間で単純にこれらの指標を比較するのは好ましくないといえる。

（注）ＢＰＴモデルについて

　ＢＰＴモデルは、ある断層の付近の応力が、（定常的に応力が蓄積する過程）＋（ブラウン運動的なランダムな擾乱）によって変化しているという仮定の下で、応力が一定のしきい値に達したときに地震が発生するというモデル。プレート運動によって次第に応力が蓄積されていく過程が第一項であり、周辺の地震活動による影響等を第二項と考えられる。

　このモデルは、例えていえば、（動く歩道）に乗った（前後不覚の酔っ払い）が歩道の端に到着するまでの時間の分布だと考えられる。到着までの平均所要時間は（歩道の長さ）÷（歩道の進む速さ）であるが、酔っ払いがたまたま前に進む歩数が多ければ早く到着し、後ろに戻る歩数が多ければ到着が遅れるので、実際の所要時間はある程度のばらつきがある。また、そのばらつきの程度の大小は酔っ払いの歩幅と歩道の長さで決まると考えられる。」

２．試案に対して寄せられた指標に関する意見・提案

　長期評価部会で「（試案）長期的な地震発生確率の評価手法及びその適用例について」（１９９８）を公表し意見を募集した際に、指標に関して後述のような意見及び提案が寄せられている。この中で、石川氏の提案については、具体的に指標を計算して、表１に示した。また、小澤氏・野本氏・山岸氏の意見は、いずれも具体的な指標の定め方についての提案ではないため、考え方によって結果は大いに変わりうる。

・石川氏の提案

　（前略）表に示されている以外の指標として、「現在より３０年後の時点での集積確率（％）を１０の単位に丸めたもの」を提案する。これは指標（３）の評価時点を現在ではなく、３０年後とするのもので、前回の地震発生時点から見て、３０年後までに地震が発生しているはずの確率になる。なお、有効数字はたかだか１桁であろうから、公表の際に２桁目以下まで示すことに意味はない。

→石川氏の提案に対する長期評価部会の考え方

　ご提案の指標は、平均活動間隔の長い断層では現在時点における集積確率とほとんど差がなく、また、それの短い断層では今後３０年間の地震発生確率と似た傾向を示す値になります。従って、試案で提案したいくつかの指標と、いくらかは重複することになります。しかしながら、興味ある提案ですので、今後の検討において新しい指標の候補にいれておきたいと思います。

・小澤氏の意見

　（前略）地震発生確率を防災情報として活用するためには、これを更に発展をさせ、例えば次のようなＡ，Ｂ，Ｃの３ランクに区別して示すなどの工夫が必要と考える。

　　　Ａランク：数年オーダーで、緊急に震災対策が必要な地震

　　　Ｂランク：数十年オーダーの中・長期的に震災対策を講じる必要のある地震

　　　Ｃランク：緊急の震災対策は必要としないが、長期的には考慮すべき地震

　（以下略）

・野本氏の意見

　（前略）・概要：指標のランク化を実施するべきではないか。

　　・趣旨：地震発生の切迫性を評価する手法として、今回の評価手法による確率の算出はわかりにくく、指標についても、印象としてストレートに理解しがたい。

　　指標については、最終的には数値によることにこだわることなく、例えばＡ〜Ｄランクのようなものにし、

　　　Ａランク：早急に地震防災対策に取り組むべきもの

　　　Ｂランク：中期的に地震防災対策に取り組むべきもの

　　　Ｃランク：長期的に地震防災対策を取り組むべきもの

　　　Ｄランク：当分の間は発生の考えられないもの

　といった指標を成果として出していくことを要望する。

・山岸氏の意見

　　確率の信頼度について

　　海域の地震と陸域の地震とでは発生間隔はもちろんそのばらつきも大いに異なるにもかかわらず、得られた地震発生確率の値をそのままう呑みにする危険性がある。

　　このため暫定的なデータとはいえ現時点で得られた最適の成果を、より効果あらしめるため指標も考慮しながら、確率の数値そのものではなく海域は海域（例えばＡ〜Ｄ）、陸域は陸域（例えばＡ’〜Ｄ’）というような４段階くらいのランク付けで表現したらいかがでしょうか。

→これらの意見に対する長期評価部会の考え方

　　一定の考え方のもとにランク付けすることは不可能ではありませんが、仮にランク付けをしても、単にそれだけで利用者が正しく理解できるわけではありませんので、前述のようにできるだけわかりやすい説明を行い、確率的な考え方を含めて理解していただくように努めたいと考えています。

　　なお、これらの意見のようにランク付けをして、そのランクに応じた対応策を講じることはもちろん重要なことです。防災関係者が、確率の数値をどのような具体的な行動に結び付けるべきかということを検討する際には協力を惜しみません。このため、中央防災会議と地震調査研究推進本部の政策委員会及び地震調査委員会の間で情報交換の場を設けるなど、地震防災対策を行う側からの要望を地震調査研究に反映させるように、地震防災対策と地震調査研究のより一層緊密な連携の具体的なあり方を検討する考えです。

３．本部会での議論を基に考案した指標の例

　本部会におけるこれまでの議論の中で、「主要活断層毎に、その活動の切迫度で順位付けをする」あるいは、「超Ａクラス、Ａクラス、Ｂクラス、Ｃクラスといったランクに分ける。分けるときに例えば、阪神・淡路大震災を起こした野島断層の地震発生時点の発生確率との比較を用いる」という考えが提起されている。

　順位付けに関しては、内陸の活断層に対する指標としては、林・島崎（１９９９）により「地震発生確率ランク」という指標が考案されている。この指標は、ある活断層について、その活断層よりも地震発生確率が高い活断層がいくつ存在するかを統計的に推測した値として定義され、ある仮定のもとに暫定的なデータを用いた計算をすると３０年確率が１０％で０〜２、５％で１０前後、３％で約３０となる。ここでは、このように概算したランクを表１に示した。また、鈴木ら（２０００）により、確率に加えて、地震が発生した場合の影響人口等を併せた危険度評価の研究が試みられている。

　過去の事例との比較については、一例として、兵庫県南部地震発生時点での野島断層の地震発生確率（Ｎ）と比較して、相当程度高ければ超Ａランク、同程度でＡランク、相当程度低ければＢランク、Ｃランクとする方法で、便宜的に、各ランクの境界値をそれぞれ仮にＮの１．５倍、１／２倍、１／１０倍方法としたものを表１に示した。ただし、ここで用いた境界値は根拠がある値ではない。

（指標の性質）

　今後３０年間に地震が発生する確率がほぼ同じで、平均活動間隔が異なる断層を仮想的に考えたものを表１に例示した。指標（１）〜（５）では、確率が高くないにもかかわらず、平均活動間隔が長いと非常危険であるかのような指標値を示すことがあったが、地震発生確率ランクやＡ〜Ｃに分類したランクではそのような矛盾は解消している。

４．災害・事故等のリスク値の例

　「（改訂試案）長期的な地震発生確率の評価手法について」には、付録として、事務局文責の解説が加えられている。ここでは「確率の利用」及び「注意喚起のための指標」の項で参考までに以下の例が引き合いに出されている。

・「今後３０年間で火災で罹災する確率」約２％

　　　根拠：平成８年の消防の統計

　　　　（火災の罹災者約９．１万人）／（人口約１億２，５００万人）×３０年

・「今後３０年間に交通事故により死亡または負傷する確率」約２０％

　　　根拠：平成８年の交通安全の統計

　　　　（道路交通事故の死者・負傷者約９５万人）／（人口約１億２，５００万人）×３０年

　このほかの災害や事故等のリスクについても見積もると、およそ次のとおりとなる。

・「今後３０年間に自宅が空き巣にあう確率」約８％

　　　根拠：平成７年の国勢調査、犯罪の統計

　　　　（住宅対象の侵入罪約１２万件）／（世帯数約４４００万）×３０年

・「今後３０年間に人に殺される確率」約０．２％

・「今後３０年間にインフルエンザで死ぬ確率」約０．１％

　　　根拠：平成１０年の死因の統計

　　　　（他殺による死亡率１０万人あたり０．６）×３０年

　　　　（インフルエンザによる死亡率１０万人あたり０．４）×３０年

・「今後３０年間に何らかの自然災害で罹災する確率」約１％

　　　根拠：平成７〜１０年の平均、警察の統計

　　　　（罹災者数年平均約５万人）／（人口約１億２，５００万人）×３０年

　　　　ただし、災害による罹災者数は年により変動が非常に大きいため、やや不正確な数値である

（災害等の確率との比較について）

　今後３０年間に地震で死亡あるいはけがをする確率ではなく、発生する確率を、災害や事故にあう確率ではなく、それが原因で死亡あるいはけがをする確率を比較することは、異種のものを比較することになるため、誤ったリスク認識を与えることになろう。また、地震発生という避けることができないものと、注意をすれば避けうるリスクを比較する場合も、同様の問題が生じる可能性がある。（防犯設備のある住宅に住む人は空き巣のリスクは比較的低く、単車に乗る人は交通事故のリスクは比較的高い）

　以上のことから、比較することが適切な事項は、慎重に選ぶ必要があると考える。

　なお、日本で発生する大地震の頻度については、次のとおり、

・日本のどこかで直下型大地震（マグニチュード７．０以上）が発生する頻度はおよそ十年に１回

　　　根拠：内陸あるいは海岸から１０ｋｍ以内で発生したマグニチュード７．０以上の地震は、

　　　　近代地震観測（１８８５年）以降で１３回

　　　　　１８９１年濃尾地震、１８９４年庄内地震、１８９６年陸羽地震、１９００年宮城県北部の地震、

　　　　　１９１４年桜島の地震、１９１４年秋田仙北地震、１９２７年北丹後地震、１９３０年北伊豆地震、

　　　　　１９４３年鳥取地震、１９４８年福井地震、１９６１年北美濃地震、１９７８年伊豆大島近海の地震、

　　　　　１９９５年兵庫県南部地震

表１　「長期的な地震発生確率」に関する指標一覧

注：現在は、２００１．０年として、それ以外は、最新の地震活動時点でＢＰＴ分布を用いた更新過程として計算した。

地震発生時期のデータセットとして、それぞれ「（改訂試案）長期的な地震発生確率の評価手法について」の南海�V、南海�W、宮城沖�V、南海�V’、牛伏寺（時間予測モデル）、阿寺�T’、丹那�T’、跡津川�T’、長野�T’、野島（時間予測モデル）を用いた。断層Ｗ〜Ｚは議論のための架空の断層。

ばらつきのパラメータとして、プレート間地震は地震発生履歴から最尤法で求めた値を、内陸の活断層については、全国共通の値μ＝０．２３を用いた。

各指標の定義は次のとおり

指標（１）：前回の地震発生時から評価時点までの経過時間（Ｂ）、指数分布（ポアッソン過程）の危険率を超えてまでの時間（Ａ）として、「年」はＢ−Ａ、「比」はＢ／Ａ

指標（２）：評価時点の危険率と、ポアッソン過程の危険率との比

指標（３）：前回の地震発生時から評価時点までの集積確率（％）

指標（４）：評価時点から３０年間での確率と、ＢＰＴ分布での収束値との比

指標（５）：ポアッソン過程での危険率（地震発生回数／年）

石川氏の意見：評価時点より３０年後の時点での集積確率（％）を１０の単位に丸めたもの

３０年確率ランク：林・島崎（１９９９）の方法で試算された、３０年確率がより高い活断層の数の推定値

クラス：野島断層の兵庫県南部地震発生時（Ｎ）における３０年確率との比較　Ｎを相当程度上回ると超Ａクラス、Ｎと同程度をＡクラス、相当程度下回るとＢｏｒＣクラス。例示のため、仮に、次のように分類。Ｎの１．５倍以上で超Ａクラス、Ｎの１／２以上でＡクラス、Ｎの１／１０以上でＢクラス、それ以下をＣクラス。

長期的な地震発生確率の各統計モデルの比較

議事次第へ戻る
地震調査研究推進本部のホームページへ戻る